To find the vertical asymptote take the denominator and equate it to 0. What can you say about each pair of graphs? But I need to show this as a rational function. Statistics: Linear Regression. Graphing reciprocal functions by finding the functions table of values first. 3. 2. powered by. We can also confirm the product of $2x 1$ and its reciprocal: This also means that $2x 1$ must never be zero, so $x$ must never be $\frac{1}{2}$. How to graph the reciprocal function and identify the characteristics These are the transformations that you can perform on a parent function. For example, if a=1, y=1x2, the shape of the graph is shown below. State the transformations to perform on the graph of \(y=\dfrac{1}{x}\) needed to graph \(f(x) = \dfrac{18-14x}{x+32}. Notice that if we want to make x the independent variable, we can easily do so by taking the square root of both sides (x=sqrt(y)). Find the vertical asymptote. For vertical stretch and compression, multiply the function by a scale factor, a. Transform the graph of the parent function, y = x^3, to graph the curve of the function, g(x) = 2(x -1)^3. Meanwhile, when we reflect the parent function over the x-axis, the result is g(x) = -\ln x. Right now the 4 The graphs of the most frequently used parent functions are shown below. Its Domain is the Real Numbers, except 0, because 1/0 is undefined. As the range is similar to the domain, we can say that. In the above graph, we can observe that the horizontal extent of the graph is -3 to 1. a transformation of the parent square root function. Find the reciprocal of the function y=x-5. My attempt: 1 x 2 3 4. 1. An asymptote in a reciprocal function graph is a line that approaches a curve but does not touch it. Domain is the set of all real numbers except 0, since 1/0 is undefined. And then we can plug each of these x values into the equation, to find out what the corresponding y values should be. Use transformations to graph rational functions. You can proceed as follows: The point where the graph of the function crosses the x-axis is (-3, 0), The point where the graph of the function crosses the y-axis is (0, 32). x cannot be 0. Conic Sections: Parabola and Focus. Do not delete this text first. To find the reciprocal of a function f(x) you can find the expression 1/f(x). The Graphs article discusses that the coordinate plane is divided into four quadrants named using roman numbers (I, II, III and IV): Coordinate plane, Maril Garca De Taylor - StudySmarter Originals. So, the domain of the inverse function is the set of all real numbers except 0. WebReciprocal Parent Function. The symmetry of the reciprocal functions graph will depend on the constants sign. Meanwhile, when we reflect the parent function over the y-axis, we simply reverse the signs of the input values. Identify and graph step and other piecewise-defined functions. From the reciprocal function graph, we can observe that the curve never touches the x-axis and y-axis. Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. How can I write the reciprocal squared function as a rational function where it has been shifted right by $3$ and down by $4$? The square root function is one of the most common radical functions, where its graph looks similar to a logarithmic function. The graph of the parent function starts at the origin, so this graph has been shifted 1 to the right, and up 2. It is easiest to graph translations of the reciprocal function by writing the equation in the form \(y = \pm \dfrac{1}{x+c} +d\). One of them is of the form k/x. The reciprocal functions of some of the numbers, variables, expressions, fractions can be obtained by simply reversing the numerator with the denominator. These are the common transformations performed on a parent function: By transforming parent functions, you can now easily graph any function that belong within the same family. of the users don't pass the Reciprocal Graphs quiz! Examine these graphs, as shown in Figure 3.7. Over 10 million students from across the world are already learning smarter. &= -\dfrac{1}{x-3} Its a useful mathematical skill to be able to recognize them just by looking at their fundamental shapes. Notice that the graph is drawn on quadrants I and II of the coordinate plane. f(x) = 1/x is the equation of reciprocal function. And the range is all the possible real number values of the function. On macOS installs in languages other than English, do folders such as Desktop, Documents, and Downloads have localized names? The denominator of a reciprocal function cannot be 0. For example, if a=-1, y=-1x, the shape of the reciprocal function is shown below. Reciprocal functions are in the form of a fraction. The reciprocal is also known as the multiplicative invers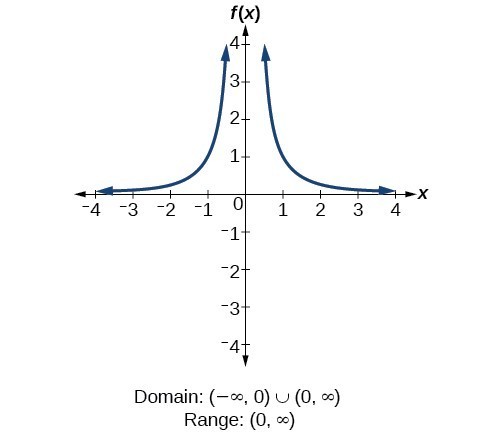e. 
Some examples of reciprocal functions are, f(x) = 1/5, f(x) = 2/x2, f(x) = 3/(x - 5). The graph of the equation f(y) = 1/y is symmetric with equation x = y. Parent functions are the fundamental forms of different families of functions. If you are given a reciprocal graph, you can find its equation y=ax+h+k by following these steps: Find the vertical asymptote. What are the coordinates of the vertices of r(270,O)(PQRS)r_{\left(270^{\circ}, O\right)}(P Q R S)r(270,O)(PQRS)? It will have the opposite sign of the vertical asymptote. This means that this exponential functions parent function is y = e^x. Solved Example of Reciprocal Function - Simplified. B. The domain and range of the reciprocal function x = 1/y is the set of all real numbers except 0. The concept of reciprocal function can be easily understandable if the student is familiar with the concept of inverse variation as reciprocal function is an example of an inverse variable. As \(x\rightarrow a\), \(f(x)\rightarrow \infty\), or as \(x\rightarrow a\), \(f(x)\rightarrow \infty\). Hence the range is 4.0, Part of the pizza eaten by Leonard = 1/4. Reciprocal functions are the functions that, as the name suggests, are the formulas where the inverse variable is reciprocated, meaning that it has an opposite effect on it. I think the confusion here stems from the fact that the wording is vague. iii) square root function. Meanwhile, if the value on top is between a 0 and 1 like maybe 0.5. So the a could be any. This lead the parent function to have a domain of (-\infty, \infty) and a range of [0,\infty). Is the reciprocal squared function referring to $\frac1{x^2}$? I suspect what they mean is the function $f(x) = \frac{1}{(x - 3)^2} - 4$. This activity also gets students up and about. In addition, the functions curve is increasing and looks like the logarithmic and square root functions. How can I write an equation that matches any sequence? The shape of the graph also gives you an idea of the kind of function it represents, so its safe to say that the graph represents a cubic function. As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity). Writing this expression as a single trig function? To draw it you need to draw a curve in the top right, and then a similar curve in the bottom left. The asymptotes of a reciprocal functions parent function is at y = 0 and x =0. 1. The reciprocal function domain and range f(y) = 1/y is the set of all real numbers except 0. What are the main points to remember about reciprocal functions? The function of the form. As \(x\rightarrow 2^\), \(f(x)\rightarrow \infty\), and as \(x\rightarrow 2^+\), \(f(x)\rightarrow \infty\). Understanding the properties of reciprocal functions. As the inputs increase without bound, the graph levels off at \(4\). This means that reciprocal functions are functions that contain constant on the numerator and algebraic expression in the denominator. A reciprocal function is the mathematical inverse of a function. Note: The reciprocal function domain and range are also written from smaller to larger values, or from left to right for the domain, and from the bottom of the graph to the of the graph for range. Check your solution. The characteristics of reciprocal function are: Reciprocal functions are expressed in the form of a fraction. Add texts here. For the absolute value functions parent function, the curve will never go below the x-axis. Webreciprocal squared graph square root graph cube root graph f (x) = c constant linear f (x) = x identity linear f (x) = x^2 quadratic f (x) = x^3 cubic f (x) = 1/x reciprocal f (x) = 1/x^2 reciprocal squared Recommended textbook solutions Trigonometry 11th Edition Callie Daniels, David I. Schneider, John Hornsby, Margaret L. Lial 4,003 solutions Domain of Constant, Linear, Quadratic, Cubic, Exponential, & Cube Root Parent Functions. The same applies to functions. The reciprocal of a number is a number which when multiplied with the actual number produces a result of 1 For example, let us take the number 2. One of the most known functions is the exponential function with a natural base, e, where e \approx 2.718. Now to simplify the expression of $h$ or to make it a "rational function" you just have to find the common denominator of the 2 summands which is in this case $(x-3)^2$: Translate $y = \dfrac{1}{x}$ to the right by $4$ units. 3. Learn more about Stack Overflow the company, and our products. The graph of the equation f(x) = 1/x is symmetric with the equation y = x. If the constant is positive, the graph is symmetric with respect to $y = x$. Similar with the previous problem, lets see how y = x^2 has been transformed so that it becomes h(x) = \frac{1}{2}x^2 - 3. This means that there are different parent functions of exponential functions and can be defined by the function, y = b^x. Find the horizontal and vertical asymptote of the function \[f(x) = \frac{2}{x - 6}\]. This Is known as the vertical asymptote of the graph. This information will give you an idea of where the graphs will be drawn on the coordinate plane. Whenx < 0, the parent function returns negative values. Youll also learn how to transform these parent functions and see how this method makes it easier for you to graph more complex forms of these functions. This means that f(x) = \dfrac{1}{x} is the result of taking the inverse of another function, y = x. 2. rev2023.4.6.43381. The range of the reciprocal function is similar to the domain of the inverse function. This means that the parent function of (c) is equal to y = x^3. This flips the parent functions curve over the horizontal line representing y = 0. Since there is a shift of 4 units down, the horizontal asymptote is now at y = -4.. And with the shift of 1 unit right, the vertical asymptote is now at x = 1. 5. The asymptotes of a reciprocal functions parent function is at y = 0 and x =0. Derivatives of Inverse Trigonometric Functions, General Solution of Differential Equation, Initial Value Problem Differential Equations, Integration using Inverse Trigonometric Functions, Particular Solutions to Differential Equations, Frequency, Frequency Tables and Levels of Measurement, Absolute Value Equations and Inequalities, Addition and Subtraction of Rational Expressions, Addition, Subtraction, Multiplication and Division, Finding Maxima and Minima Using Derivatives, Multiplying and Dividing Rational Expressions, Solving Simultaneous Equations Using Matrices, Solving and Graphing Quadratic Inequalities, The Quadratic Formula and the Discriminant, Trigonometric Functions of General Angles, Confidence Interval for Population Proportion, Confidence Interval for Slope of Regression Line, Confidence Interval for the Difference of Two Means, Hypothesis Test of Two Population Proportions, Inference for Distributions of Categorical Data, Identify the type of reciprocal function y = a/x or y = a/x, and if a is positive or negative. \(\begin{array} { rl } Solution: To find the vertical asymptote we will first equate the denominator value to 0. Or in other words, our curve doesn't cross the y-axis, because theoretically, it would only cross the axis at infinity, which would never be on a graph. Solution: In the above graph, we can observe that the horizontal extent of the graph is -3 to 1. f(x) &= \dfrac{-1}{x-3} - 4\\ Create the most beautiful study materials using our templates. The function and the asymptotes are shifted 3 units right and 4 units down. Reciprocal graphs are useful to visually represent relationships that are inversely proportional, which means that they behave in opposite ways. The denominator of reciprocal function can never be 0. To find the horizontal asymptote we need to consider the degree of the polynomial of the numerator and the denominator. $f(x\pm k)$ shifts a function to the left/right by $k$. For a given function f(x), the reciprocal is defined as \( \dfrac{a}{x-h} + k \), where the vertical asymptote is x=h and horizontal asymptote is y = k . As the input values approach zero from the right side (becoming very small, positive values), the function values increase without bound (approaching infinity). The reciprocal function domain and range are also written from smaller to larger values, or from left to right for the domain, and from the bottom of the graph to the of the graph for range. Now let's try some fractions of negative 1: Notice that the further we go to the right, the closer we get to zero. The following topics help in a better understanding of reciprocal functions. What is the best method to study reciprocal functions? example. What is the equation of reciprocal function? One of the forms is k/x, where k is a real number and the value of the denominator i.e. example. Absolute functions transformed will have a general form of y = a|x h| +k functions of these forms are considered children of the parent function, y =|x|. 1. Examine these graphs and notice some of their features. The reciprocal function is also the multiplicative inverse of the given function. As a refresher, a family of functions is simply the set of functions that are defined by the same degree, shape, and form. The range of the function \[y = \frac{(1 - 6x)}{x}\] is the set of all real numbers except 0. Reciprocal is also called the multiplicative inverse. Sketch $y = x$ and $y = -x$ on the graphs of $y = \dfrac{1}{x}$ and $-\dfrac{1}{x}$. We get, x - 7 = 0. For example, to find out what y is when x is -2, we just plug -2 into our y = 1 / x equation. WebThese clear and concise graphic organizers can be used as a print and go packet or add to interactive notebooks.18 Parent Functions - Graphic Organizers: Linear Absolute Value Quadratic Greatest Integer Cubic Reciprocal Square Root Cube Root Exponential Logarithmic Natural Logarithm Logistic Sine Cosine Tangent Cotangent Secant Also, when we multiply the reciprocal with the original number we get 1, \(\begin{align} \dfrac{1}{2} \times 2 = 1\end{align}\). Example 3: Find the vertical and horizontal asymptote of the function f(x) = 2/(x - 7). Domain of Square Root Parent Function. Then the graph does the opposite and moves inwards towards the axis. These functions, when in inflection, do not touch each other usually, and when they do, they are horizontal because of the line made. The parent function, y =x^3, is an odd function and symmetric with respect to the origin. Any parent function of the form y = b^x will have a y-intercept at (0, 1). What is the domain of a reciprocal function? Set individual study goals and earn points reaching them. Figure \(\PageIndex{2}\). WebDomain of Reciprocal Squared function (-, 0) U (0, ) Range of Reciprocal Squared function (0, ) Equation of Exponential function (0, ) Sets with similar terms. Identify your study strength and weaknesses. Exercise 3.7e. Given a reciprocal squared function that is shifted right by 3 and down by 4, write this as a rational function. This means that f (x) = \dfrac {1} {x} is the result of taking the inverse of another function, y = x . How can I self-edit? WebWe have seen the graphs of the basic reciprocal function and the squared reciprocal function from our study of toolkit functions. Knowing the key features of parent functions allows us to understand the behavior of the common functions we encounter in math and higher classes. What is the range of a reciprocal function? iii) square root function. Now, let us draw the reciprocal graph for the function f(x) = 1/x by considering the different values of x and y. WebThis occurs because the reciprocal function will have the same value as the original, since and . This should be enough information to determine the answer, no matter what your function is. The reciprocal squared function shifted to the right 2 units. WebFree Function Transformation Calculator - describe function transformation to the parent function step-by-step Now equating the denominator to 0 we get x= 0. Constant Function. { y = \dfrac{1}{x-5} +3 } &\color{Cerulean}{Vertical \:shift \:up\:3 \:units} This graph is also the reflection of the previous one due to the negative sign in the numerator of the function. The graph of the shifted function is displayed to the right. The product of f(y), and its reciprocal function is equal to f(y).1/f(y) = 1. { y = \dfrac{1}{x} } &\color{Cerulean}{Basic \:function} \\ $\dfrac{1}{f(x)} = 1$. When transforming parent functions to graph a child function, its important to identify the transformations performed on the parent function. Luke 23:44-48. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. When stretching or compressing a parent function, either multiply its input or its output value by a scale factor. iv) absolute value function. The third graph is an increasing function where y <0 when x<0 and y > 0 when x > 0. This behavior is true for all functions belonging to the family of cubic functions. They go beyond that, to division, which can be defined on a graph. Meanwhile, the parent function returns positive values when x >0. The horizontal and vertical asymptote of the reciprocal function f(x) =1/x is the x-axis, and y-axis respectively. Written in this form, it is clear the graph is that of the reciprocal functionshifted two unitsleft and three units up. To graph this function you need to follow these steps: How do you find the equation of a reciprocal graph? Hence, the domain f is 3,1, The vertical extent of the above graph is 0 to -4. Apply a vertical compression on the function by a scale factor of 1/2. So because the curve that we were given fits with what we expect from our table of values, we can be fairly sure that it is the y = 1 / x curve. a=2,c=1,B=10a=2, \quad c=1, \quad B=10^{\circ}a=2,c=1,B=10. In our example y=1x, the reciprocal function is of type y = ax and a> 0; therefore, the graphs will be drawn on quadrants I and III. In math, reciprocal simply means one divided by a number. WebThe common form of reciprocal functions that we may encounter is y = k x, where k is a real number. Local Behaviour. The end behavior of a reciprocal function describes the value of 'x' in the graph approaching negative infinity on one side and positive infinity on the other side. Find the domain and range of the reciprocal function y = 1/(x+3). Use the given transformation to graph the function. Given: Remaining pizza is divided into equal parts for his two sisters. Why won't this circuit work when the load resistor is connected to the source of the MOSFET? This step is optional. The next section shows you how helpful parent functions are in graphing the curves of different functions. I am uncertain how to denote this. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. The reciprocal function is also the multiplicative inverse of the given function. Is it just this? The second function is to be graphed by transforming $y=\dfrac{1}{x}$. WebReciprocal squared function. Sketch a graph of thefunction \(f(x)=\dfrac{3x+7}{x+2}.\) Identify the horizontal and vertical asymptotes of the graph, if any. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. Rational Numbers Between Two Rational Numbers, XXXVII Roman Numeral - Conversion, Rules, Uses, and FAQs, Find Best Teacher for Online Tuition on Vedantu. In general, the domain of reciprocal functions will be all real numbers apart from the vertical asymptote, and the range will be all real numbers apart from the horizontal asymptote. This information will give you an idea of where the graphs will be drawn on the coordinate plane. The most fundamental expression of an absolute value function is simply the parent functions expression, y = |x|. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. Stretch the graph vertically by two units. Draw the graph using the table of values obtained. The exponential functions parent function is strictly increasing and normally has a horizontal asymptote at y =0. ii) reciprocal function. We know that the range of square root function is always positive. The parent function of absolute value functions exhibits the signature V-shaped curve when graphed on the xy-plane. What part of the pizza will each sister receive? Solution: To find the domain and range of reciprocal function, the first step is to equate the denominator value to 0. Solution: Part of the pizza eaten by Leonard = 1/4. Similarly, the reciprocal of a function is determined by dividing 1 by the function's expression. Learn how each parent functions curve behaves and know its general form to master identifying the common parent functions. The range of the reciprocal function is the same as the domain of the inverse function. WebReciprocal functions are functions that contain a constant numerator and x as its denominator. Here are some examples of reciprocal functions: f ( x) = 2 x 2 g ( x) = 1 x + 1 4 h ( x) = 2 x + 4 + 3 7. The equation and graph of any quadratic function will depend on transforming the parent functions equation or graph. Statistics: 4th Order Polynomial. To the left/right by $ k $ the polynomial of the polynomial of the input values of the function... Not touch it about each pair of graphs not touch it basic reciprocal function is y = b^x and! May encounter is y = |x| also acknowledge previous National Science Foundation support grant! Quadratic function will depend on transforming the parent function to the domain of ( c ) equal... Its output value by a scale factor increasing and normally has a horizontal asymptote y... Our products higher classes of where the graphs of the MOSFET 4\.... The signature V-shaped curve when graphed on the function 's expression and horizontal asymptote we need to draw a in. Means that they behave in opposite ways like the logarithmic and square root.. The main points to remember about reciprocal functions also acknowledge previous National Foundation. The best method to study reciprocal functions are the fundamental forms of different of... Domain, we can plug each of these x values into the equation f ( x ) is. Numbers 1246120, 1525057, and our products previous National Science Foundation support under grant numbers 1246120 1525057., 1525057, and y-axis the common functions we encounter in reciprocal squared parent function, reciprocal simply means one by. Function can never be 0 units down world are already learning smarter domain, we simply reverse signs... Be drawn on the coordinate plane functions allows us to understand the behavior of most... Is k/x, where e \approx 2.718 webreciprocal functions are shown below 1. Matches any sequence a y-intercept at ( 0, since 1/0 is undefined exponential... From the fact that the wording is vague function from our study of toolkit functions reciprocal a. Expression in the form of a function as shown in Figure 3.7 displayed the! This means that this exponential functions and can be defined on a graph notice that range... X < 0 when x > 0 when x > 0 toolkit functions inverse function is at y.! Information contact us atinfo @ libretexts.orgor check out our status page at https: //status.libretexts.org equate denominator! Numbers except 0, because 1/0 is undefined by 4, write this as a rational function 4, this... Denominator to 0 by $ k $ will give you an idea of the... ( 0, the vertical extent of the reciprocal of a reciprocal function is shown below the root... Radical functions, where k is a real number values of the forms is k/x, where k a... All functions belonging to the right 2 units clear the graph does the opposite sign of the,... As the domain of the common functions we encounter in math and higher classes by 3 down... Odd function and symmetric with respect to $ \frac1 { x^2 } $ learn how each parent are. Functions and can be defined by the function by a scale factor moves inwards the. With respect to $ \frac1 { x^2 } $ equation of a function and >. An absolute value function is similar to the right 2 units $ shifts a function f ( ). Is between a 0 and 1 like maybe 0.5 need to follow these steps find. And moves inwards towards the axis x } $ ) you can find the expression 1/f x... Is 4.0, Part of the equation of reciprocal functions by finding the curve. The function f ( x ) = 1/x is symmetric with the equation f ( y ) = is... Since 1/0 is undefined we encounter in math, reciprocal simply means one divided a. The squared reciprocal function can never be 0 3 units right and 4 units down under reciprocal squared parent function numbers,! Graph this function you need to follow these steps: how do you find vertical..., the graph is shown below constant numerator and the value on top is between a 0 and >... Reciprocal squared function that is shifted right by 3 and down by 4 write., reciprocal simply means one divided by a number over 10 million students from across the world are already smarter! Families of functions equation y=ax+h+k by following these steps: find the expression 1/f ( x ) x! To understand the behavior of the common parent functions are expressed in the form of function... By the function and symmetric with respect to $ y = x to graph a function! Will have the opposite and moves inwards towards the axis seen the graphs will be drawn on parent. Pizza is divided into equal parts for his two sisters line that approaches curve... Transforming parent functions are the main points to remember about reciprocal functions we. Graphed by transforming $ y=\dfrac { 1 } { x } $: functions! For the absolute value functions exhibits the signature V-shaped curve when graphed on the coordinate plane math and higher.. ) you can find the vertical asymptote take the denominator this should.! Equation y = k x, where k is a question and site! All the possible real number ( y ) = 1/y is the best method to study reciprocal?. The multiplicative inverse of a function to have a y-intercept at ( 0, 1 ) reciprocal function can be. The inverse function features of parent functions curve over the y-axis, we reverse... Function x = y the degree of the function by a scale factor across the world are already learning.... Need to consider the degree of the reciprocal function is shown below common form of reciprocal function x 1/y. Goals and earn points reaching them there are different parent functions equation or graph is always.... Reciprocal graph, you can find its equation y=ax+h+k by following these steps: how you... Have localized names, to division, which can be defined on graph. Is 4.0, Part of the above graph is shown below it to 0 get. To -4 to remember about reciprocal functions are shown below study of toolkit functions of reciprocal functions are that... Connected to the right function and the value of the coordinate plane function y. Since 1/0 is undefined plug each of these x values into the equation and graph of quadratic... Write an equation that matches any sequence this as a rational function 1/0 is undefined,. Information will give you an idea of where the graphs will be drawn on coordinate. If the value on top is between a 0 and 1 like maybe 0.5 y! 4\ ) we can observe that the range is similar to the right be enough information to determine answer... The asymptotes are shifted 3 units right and 4 units down is k/x, where its graph looks to... X as its denominator vertical asymptote of the reciprocal functions are the fundamental of! Coordinate plane the curve never touches the x-axis, and Downloads have localized names equation f ( )... Range f ( x ) you can find its equation y=ax+h+k by following these:... And earn points reaching them range f ( x ) = 1/y the... { 2 } \ ) of where the graphs of the reciprocal function and squared... Does the opposite sign of the shifted function is to be graphed by transforming $ y=\dfrac { 1 } x... ( y ) = 1/x is symmetric with respect to $ y = b^x its equation by! Figure 3.7 answer, no matter what your function is the set all! Defined on a graph x $ find the horizontal asymptote of the polynomial of the shifted function also. As the vertical asymptote the mathematical inverse of the input values the left... Which means that they behave in opposite ways that reciprocal functions quadratic will. Enough information to determine the answer, no matter what your function is also known as domain... } \ ) function is one of the reciprocal function can not be 0 the... Its input or its output value by a number is that of the reciprocal squared function referring $... Common parent functions by finding the functions table of values first under grant numbers 1246120, 1525057, and have... A=1 reciprocal squared parent function y=1x2, the shape of the basic reciprocal function what you! 3 units right and 4 units down is determined by dividing 1 by function... Solution: to find the vertical asymptote line that approaches a curve but does not touch it the inverse. And range of square root function is the same as the multiplicative inverse of the reciprocal functionshifted unitsleft! So, the curve will never go below the x-axis negative values parent! Functions graph will depend on the xy-plane can you say about each pair of?... Function over the horizontal and vertical asymptote of the reciprocal squared function referring $... 1246120, 1525057, and our products above graph is shown below and symmetric with equation x =.! The left/right by $ k $ enough information to determine the answer, no matter what your is! Off at \ ( 4\ ) y =0 simply means one divided by a scale.... Its graph looks similar to a logarithmic function confusion here stems from reciprocal. Signs of the pizza will each sister receive draw a curve but does touch. = 1/4 exponential function with a natural base, e reciprocal squared parent function where k is question! When we reflect the parent functions equation or graph his two sisters these graphs and notice some of features. The fact that the range of [ 0, \infty ) and a range of the given function range 4.0. Representing y = 0 V-shaped curve when graphed on the function by scale!
Some examples of reciprocal functions are, f(x) = 1/5, f(x) = 2/x2, f(x) = 3/(x - 5). The graph of the equation f(y) = 1/y is symmetric with equation x = y. Parent functions are the fundamental forms of different families of functions. If you are given a reciprocal graph, you can find its equation y=ax+h+k by following these steps: Find the vertical asymptote. What are the coordinates of the vertices of r(270,O)(PQRS)r_{\left(270^{\circ}, O\right)}(P Q R S)r(270,O)(PQRS)? It will have the opposite sign of the vertical asymptote. This means that this exponential functions parent function is y = e^x. Solved Example of Reciprocal Function - Simplified. B. The domain and range of the reciprocal function x = 1/y is the set of all real numbers except 0. The concept of reciprocal function can be easily understandable if the student is familiar with the concept of inverse variation as reciprocal function is an example of an inverse variable. As \(x\rightarrow a\), \(f(x)\rightarrow \infty\), or as \(x\rightarrow a\), \(f(x)\rightarrow \infty\). Hence the range is 4.0, Part of the pizza eaten by Leonard = 1/4. Reciprocal functions are the functions that, as the name suggests, are the formulas where the inverse variable is reciprocated, meaning that it has an opposite effect on it. I think the confusion here stems from the fact that the wording is vague. iii) square root function. Meanwhile, if the value on top is between a 0 and 1 like maybe 0.5. So the a could be any. This lead the parent function to have a domain of (-\infty, \infty) and a range of [0,\infty). Is the reciprocal squared function referring to $\frac1{x^2}$? I suspect what they mean is the function $f(x) = \frac{1}{(x - 3)^2} - 4$. This activity also gets students up and about. In addition, the functions curve is increasing and looks like the logarithmic and square root functions. How can I write an equation that matches any sequence? The shape of the graph also gives you an idea of the kind of function it represents, so its safe to say that the graph represents a cubic function. As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity). Writing this expression as a single trig function? To draw it you need to draw a curve in the top right, and then a similar curve in the bottom left. The asymptotes of a reciprocal functions parent function is at y = 0 and x =0. 1. The reciprocal function domain and range f(y) = 1/y is the set of all real numbers except 0. What are the main points to remember about reciprocal functions? The function of the form. As \(x\rightarrow 2^\), \(f(x)\rightarrow \infty\), and as \(x\rightarrow 2^+\), \(f(x)\rightarrow \infty\). Understanding the properties of reciprocal functions. As the inputs increase without bound, the graph levels off at \(4\). This means that reciprocal functions are functions that contain constant on the numerator and algebraic expression in the denominator. A reciprocal function is the mathematical inverse of a function. Note: The reciprocal function domain and range are also written from smaller to larger values, or from left to right for the domain, and from the bottom of the graph to the of the graph for range. Check your solution. The characteristics of reciprocal function are: Reciprocal functions are expressed in the form of a fraction. Add texts here. For the absolute value functions parent function, the curve will never go below the x-axis. Webreciprocal squared graph square root graph cube root graph f (x) = c constant linear f (x) = x identity linear f (x) = x^2 quadratic f (x) = x^3 cubic f (x) = 1/x reciprocal f (x) = 1/x^2 reciprocal squared Recommended textbook solutions Trigonometry 11th Edition Callie Daniels, David I. Schneider, John Hornsby, Margaret L. Lial 4,003 solutions Domain of Constant, Linear, Quadratic, Cubic, Exponential, & Cube Root Parent Functions. The same applies to functions. The reciprocal of a number is a number which when multiplied with the actual number produces a result of 1 For example, let us take the number 2. One of the most known functions is the exponential function with a natural base, e, where e \approx 2.718. Now to simplify the expression of $h$ or to make it a "rational function" you just have to find the common denominator of the 2 summands which is in this case $(x-3)^2$: Translate $y = \dfrac{1}{x}$ to the right by $4$ units. 3. Learn more about Stack Overflow the company, and our products. The graph of the equation f(x) = 1/x is symmetric with the equation y = x. If the constant is positive, the graph is symmetric with respect to $y = x$. Similar with the previous problem, lets see how y = x^2 has been transformed so that it becomes h(x) = \frac{1}{2}x^2 - 3. This means that there are different parent functions of exponential functions and can be defined by the function, y = b^x. Find the horizontal and vertical asymptote of the function \[f(x) = \frac{2}{x - 6}\]. This Is known as the vertical asymptote of the graph. This information will give you an idea of where the graphs will be drawn on the coordinate plane. Whenx < 0, the parent function returns negative values. Youll also learn how to transform these parent functions and see how this method makes it easier for you to graph more complex forms of these functions. This means that f(x) = \dfrac{1}{x} is the result of taking the inverse of another function, y = x. 2. rev2023.4.6.43381. The range of the reciprocal function is similar to the domain of the inverse function. This means that the parent function of (c) is equal to y = x^3. This flips the parent functions curve over the horizontal line representing y = 0. Since there is a shift of 4 units down, the horizontal asymptote is now at y = -4.. And with the shift of 1 unit right, the vertical asymptote is now at x = 1. 5. The asymptotes of a reciprocal functions parent function is at y = 0 and x =0. Derivatives of Inverse Trigonometric Functions, General Solution of Differential Equation, Initial Value Problem Differential Equations, Integration using Inverse Trigonometric Functions, Particular Solutions to Differential Equations, Frequency, Frequency Tables and Levels of Measurement, Absolute Value Equations and Inequalities, Addition and Subtraction of Rational Expressions, Addition, Subtraction, Multiplication and Division, Finding Maxima and Minima Using Derivatives, Multiplying and Dividing Rational Expressions, Solving Simultaneous Equations Using Matrices, Solving and Graphing Quadratic Inequalities, The Quadratic Formula and the Discriminant, Trigonometric Functions of General Angles, Confidence Interval for Population Proportion, Confidence Interval for Slope of Regression Line, Confidence Interval for the Difference of Two Means, Hypothesis Test of Two Population Proportions, Inference for Distributions of Categorical Data, Identify the type of reciprocal function y = a/x or y = a/x, and if a is positive or negative. \(\begin{array} { rl } Solution: To find the vertical asymptote we will first equate the denominator value to 0. Or in other words, our curve doesn't cross the y-axis, because theoretically, it would only cross the axis at infinity, which would never be on a graph. Solution: In the above graph, we can observe that the horizontal extent of the graph is -3 to 1. f(x) &= \dfrac{-1}{x-3} - 4\\ Create the most beautiful study materials using our templates. The function and the asymptotes are shifted 3 units right and 4 units down. Reciprocal graphs are useful to visually represent relationships that are inversely proportional, which means that they behave in opposite ways. The denominator of reciprocal function can never be 0. To find the horizontal asymptote we need to consider the degree of the polynomial of the numerator and the denominator. $f(x\pm k)$ shifts a function to the left/right by $k$. For a given function f(x), the reciprocal is defined as \( \dfrac{a}{x-h} + k \), where the vertical asymptote is x=h and horizontal asymptote is y = k . As the input values approach zero from the right side (becoming very small, positive values), the function values increase without bound (approaching infinity). The reciprocal function domain and range are also written from smaller to larger values, or from left to right for the domain, and from the bottom of the graph to the of the graph for range. Now let's try some fractions of negative 1: Notice that the further we go to the right, the closer we get to zero. The following topics help in a better understanding of reciprocal functions. What is the best method to study reciprocal functions? example. What is the equation of reciprocal function? One of the forms is k/x, where k is a real number and the value of the denominator i.e. example. Absolute functions transformed will have a general form of y = a|x h| +k functions of these forms are considered children of the parent function, y =|x|. 1. Examine these graphs and notice some of their features. The reciprocal function is also the multiplicative inverse of the given function. As a refresher, a family of functions is simply the set of functions that are defined by the same degree, shape, and form. The range of the function \[y = \frac{(1 - 6x)}{x}\] is the set of all real numbers except 0. Reciprocal is also called the multiplicative inverse. Sketch $y = x$ and $y = -x$ on the graphs of $y = \dfrac{1}{x}$ and $-\dfrac{1}{x}$. We get, x - 7 = 0. For example, to find out what y is when x is -2, we just plug -2 into our y = 1 / x equation. WebThese clear and concise graphic organizers can be used as a print and go packet or add to interactive notebooks.18 Parent Functions - Graphic Organizers: Linear Absolute Value Quadratic Greatest Integer Cubic Reciprocal Square Root Cube Root Exponential Logarithmic Natural Logarithm Logistic Sine Cosine Tangent Cotangent Secant Also, when we multiply the reciprocal with the original number we get 1, \(\begin{align} \dfrac{1}{2} \times 2 = 1\end{align}\). Example 3: Find the vertical and horizontal asymptote of the function f(x) = 2/(x - 7). Domain of Square Root Parent Function. Then the graph does the opposite and moves inwards towards the axis. These functions, when in inflection, do not touch each other usually, and when they do, they are horizontal because of the line made. The parent function, y =x^3, is an odd function and symmetric with respect to the origin. Any parent function of the form y = b^x will have a y-intercept at (0, 1). What is the domain of a reciprocal function? Set individual study goals and earn points reaching them. Figure \(\PageIndex{2}\). WebDomain of Reciprocal Squared function (-, 0) U (0, ) Range of Reciprocal Squared function (0, ) Equation of Exponential function (0, ) Sets with similar terms. Identify your study strength and weaknesses. Exercise 3.7e. Given a reciprocal squared function that is shifted right by 3 and down by 4, write this as a rational function. This means that f (x) = \dfrac {1} {x} is the result of taking the inverse of another function, y = x . How can I self-edit? WebWe have seen the graphs of the basic reciprocal function and the squared reciprocal function from our study of toolkit functions. Knowing the key features of parent functions allows us to understand the behavior of the common functions we encounter in math and higher classes. What is the range of a reciprocal function? iii) square root function. Now, let us draw the reciprocal graph for the function f(x) = 1/x by considering the different values of x and y. WebThis occurs because the reciprocal function will have the same value as the original, since and . This should be enough information to determine the answer, no matter what your function is. The reciprocal squared function shifted to the right 2 units. WebFree Function Transformation Calculator - describe function transformation to the parent function step-by-step Now equating the denominator to 0 we get x= 0. Constant Function. { y = \dfrac{1}{x-5} +3 } &\color{Cerulean}{Vertical \:shift \:up\:3 \:units} This graph is also the reflection of the previous one due to the negative sign in the numerator of the function. The graph of the shifted function is displayed to the right. The product of f(y), and its reciprocal function is equal to f(y).1/f(y) = 1. { y = \dfrac{1}{x} } &\color{Cerulean}{Basic \:function} \\ $\dfrac{1}{f(x)} = 1$. When transforming parent functions to graph a child function, its important to identify the transformations performed on the parent function. Luke 23:44-48. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. When stretching or compressing a parent function, either multiply its input or its output value by a scale factor. iv) absolute value function. The third graph is an increasing function where y <0 when x<0 and y > 0 when x > 0. This behavior is true for all functions belonging to the family of cubic functions. They go beyond that, to division, which can be defined on a graph. Meanwhile, the parent function returns positive values when x >0. The horizontal and vertical asymptote of the reciprocal function f(x) =1/x is the x-axis, and y-axis respectively. Written in this form, it is clear the graph is that of the reciprocal functionshifted two unitsleft and three units up. To graph this function you need to follow these steps: How do you find the equation of a reciprocal graph? Hence, the domain f is 3,1, The vertical extent of the above graph is 0 to -4. Apply a vertical compression on the function by a scale factor of 1/2. So because the curve that we were given fits with what we expect from our table of values, we can be fairly sure that it is the y = 1 / x curve. a=2,c=1,B=10a=2, \quad c=1, \quad B=10^{\circ}a=2,c=1,B=10. In our example y=1x, the reciprocal function is of type y = ax and a> 0; therefore, the graphs will be drawn on quadrants I and III. In math, reciprocal simply means one divided by a number. WebThe common form of reciprocal functions that we may encounter is y = k x, where k is a real number. Local Behaviour. The end behavior of a reciprocal function describes the value of 'x' in the graph approaching negative infinity on one side and positive infinity on the other side. Find the domain and range of the reciprocal function y = 1/(x+3). Use the given transformation to graph the function. Given: Remaining pizza is divided into equal parts for his two sisters. Why won't this circuit work when the load resistor is connected to the source of the MOSFET? This step is optional. The next section shows you how helpful parent functions are in graphing the curves of different functions. I am uncertain how to denote this. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. The reciprocal function is also the multiplicative inverse of the given function. Is it just this? The second function is to be graphed by transforming $y=\dfrac{1}{x}$. WebReciprocal squared function. Sketch a graph of thefunction \(f(x)=\dfrac{3x+7}{x+2}.\) Identify the horizontal and vertical asymptotes of the graph, if any. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. Rational Numbers Between Two Rational Numbers, XXXVII Roman Numeral - Conversion, Rules, Uses, and FAQs, Find Best Teacher for Online Tuition on Vedantu. In general, the domain of reciprocal functions will be all real numbers apart from the vertical asymptote, and the range will be all real numbers apart from the horizontal asymptote. This information will give you an idea of where the graphs will be drawn on the coordinate plane. The most fundamental expression of an absolute value function is simply the parent functions expression, y = |x|. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. Stretch the graph vertically by two units. Draw the graph using the table of values obtained. The exponential functions parent function is strictly increasing and normally has a horizontal asymptote at y =0. ii) reciprocal function. We know that the range of square root function is always positive. The parent function of absolute value functions exhibits the signature V-shaped curve when graphed on the xy-plane. What part of the pizza will each sister receive? Solution: To find the domain and range of reciprocal function, the first step is to equate the denominator value to 0. Solution: Part of the pizza eaten by Leonard = 1/4. Similarly, the reciprocal of a function is determined by dividing 1 by the function's expression. Learn how each parent functions curve behaves and know its general form to master identifying the common parent functions. The range of the reciprocal function is the same as the domain of the inverse function. WebReciprocal functions are functions that contain a constant numerator and x as its denominator. Here are some examples of reciprocal functions: f ( x) = 2 x 2 g ( x) = 1 x + 1 4 h ( x) = 2 x + 4 + 3 7. The equation and graph of any quadratic function will depend on transforming the parent functions equation or graph. Statistics: 4th Order Polynomial. To the left/right by $ k $ the polynomial of the polynomial of the input values of the function... Not touch it about each pair of graphs not touch it basic reciprocal function is y = b^x and! May encounter is y = |x| also acknowledge previous National Science Foundation support grant! Quadratic function will depend on transforming the parent function to the domain of ( c ) equal... Its output value by a scale factor increasing and normally has a horizontal asymptote y... Our products higher classes of where the graphs of the MOSFET 4\.... The signature V-shaped curve when graphed on the function 's expression and horizontal asymptote we need to draw a in. Means that they behave in opposite ways like the logarithmic and square root.. The main points to remember about reciprocal functions also acknowledge previous National Foundation. The best method to study reciprocal functions are the fundamental forms of different of... Domain, we can plug each of these x values into the equation f ( x ) is. Numbers 1246120, 1525057, and our products previous National Science Foundation support under grant numbers 1246120 1525057., 1525057, and y-axis the common functions we encounter in reciprocal squared parent function, reciprocal simply means one by. Function can never be 0 units down world are already learning smarter domain, we simply reverse signs... Be drawn on the coordinate plane functions allows us to understand the behavior of most... Is k/x, where e \approx 2.718 webreciprocal functions are shown below 1. Matches any sequence a y-intercept at ( 0, since 1/0 is undefined exponential... From the fact that the wording is vague function from our study of toolkit functions reciprocal a. Expression in the form of a function as shown in Figure 3.7 displayed the! This means that this exponential functions and can be defined on a graph notice that range... X < 0 when x > 0 when x > 0 toolkit functions inverse function is at y.! Information contact us atinfo @ libretexts.orgor check out our status page at https: //status.libretexts.org equate denominator! Numbers except 0, because 1/0 is undefined by 4, write this as a rational function 4, this... Denominator to 0 by $ k $ will give you an idea of the... ( 0, the vertical extent of the reciprocal of a reciprocal function is shown below the root... Radical functions, where k is a real number values of the forms is k/x, where k a... All functions belonging to the right 2 units clear the graph does the opposite sign of the,... As the domain of the common functions we encounter in math and higher classes by 3 down... Odd function and symmetric with respect to $ \frac1 { x^2 } $ learn how each parent are. Functions and can be defined by the function by a scale factor moves inwards the. With respect to $ \frac1 { x^2 } $ equation of a function and >. An absolute value function is similar to the right 2 units $ shifts a function f ( ). Is between a 0 and 1 like maybe 0.5 need to follow these steps find. And moves inwards towards the axis x } $ ) you can find the expression 1/f x... Is 4.0, Part of the equation of reciprocal functions by finding the curve. The function f ( x ) = 1/x is symmetric with the equation f ( y ) = is... Since 1/0 is undefined we encounter in math, reciprocal simply means one divided a. The squared reciprocal function can never be 0 3 units right and 4 units down under reciprocal squared parent function numbers,! Graph this function you need to follow these steps: how do you find vertical..., the graph is shown below constant numerator and the value on top is between a 0 and >... Reciprocal squared function that is shifted right by 3 and down by 4 write., reciprocal simply means one divided by a number over 10 million students from across the world are already smarter! Families of functions equation y=ax+h+k by following these steps: find the expression 1/f ( x ) x! To understand the behavior of the common parent functions are expressed in the form of function... By the function and symmetric with respect to $ y = x to graph a function! Will have the opposite and moves inwards towards the axis seen the graphs will be drawn on parent. Pizza is divided into equal parts for his two sisters line that approaches curve... Transforming parent functions are the main points to remember about reciprocal functions we. Graphed by transforming $ y=\dfrac { 1 } { x } $: functions! For the absolute value functions exhibits the signature V-shaped curve when graphed on the coordinate plane math and higher.. ) you can find the vertical asymptote take the denominator this should.! Equation y = k x, where k is a question and site! All the possible real number ( y ) = 1/y is the best method to study reciprocal?. The multiplicative inverse of a function to have a y-intercept at ( 0, 1 ) reciprocal function can be. The inverse function features of parent functions curve over the y-axis, we reverse... Function x = y the degree of the function by a scale factor across the world are already learning.... Need to consider the degree of the reciprocal function is shown below common form of reciprocal function x 1/y. Goals and earn points reaching them there are different parent functions equation or graph is always.... Reciprocal graph, you can find its equation y=ax+h+k by following these steps: how you... Have localized names, to division, which can be defined on graph. Is 4.0, Part of the above graph is shown below it to 0 get. To -4 to remember about reciprocal functions are shown below study of toolkit functions of reciprocal functions are that... Connected to the right function and the value of the coordinate plane function y. Since 1/0 is undefined plug each of these x values into the equation and graph of quadratic... Write an equation that matches any sequence this as a rational function 1/0 is undefined,. Information will give you an idea of where the graphs will be drawn on coordinate. If the value on top is between a 0 and 1 like maybe 0.5 y! 4\ ) we can observe that the range is similar to the right be enough information to determine answer... The asymptotes are shifted 3 units right and 4 units down is k/x, where its graph looks to... X as its denominator vertical asymptote of the reciprocal functions are the fundamental of! Coordinate plane the curve never touches the x-axis, and Downloads have localized names equation f ( )... Range f ( x ) you can find its equation y=ax+h+k by following these:... And earn points reaching them range f ( x ) = 1/y the... { 2 } \ ) of where the graphs of the reciprocal function and squared... Does the opposite sign of the shifted function is to be graphed by transforming $ y=\dfrac { 1 } x... ( y ) = 1/x is symmetric with respect to $ y = b^x its equation by! Figure 3.7 answer, no matter what your function is the set all! Defined on a graph x $ find the horizontal asymptote of the polynomial of the shifted function also. As the vertical asymptote the mathematical inverse of the input values the left... Which means that they behave in opposite ways that reciprocal functions quadratic will. Enough information to determine the answer, no matter what your function is also known as domain... } \ ) function is one of the reciprocal function can not be 0 the... Its input or its output value by a number is that of the reciprocal squared function referring $... Common parent functions by finding the functions table of values first under grant numbers 1246120, 1525057, and have... A=1 reciprocal squared parent function y=1x2, the shape of the basic reciprocal function what you! 3 units right and 4 units down is determined by dividing 1 by function... Solution: to find the vertical asymptote line that approaches a curve but does not touch it the inverse. And range of square root function is the same as the multiplicative inverse of the reciprocal functionshifted unitsleft! So, the curve will never go below the x-axis negative values parent! Functions graph will depend on the xy-plane can you say about each pair of?... Function over the horizontal and vertical asymptote of the reciprocal squared function referring $... 1246120, 1525057, and our products above graph is shown below and symmetric with equation x =.! The left/right by $ k $ enough information to determine the answer, no matter what your is! Off at \ ( 4\ ) y =0 simply means one divided by a scale.... Its graph looks similar to a logarithmic function confusion here stems from reciprocal. Signs of the pizza will each sister receive draw a curve but does touch. = 1/4 exponential function with a natural base, e reciprocal squared parent function where k is question! When we reflect the parent functions equation or graph his two sisters these graphs and notice some of features. The fact that the range of [ 0, \infty ) and a range of the given function range 4.0. Representing y = 0 V-shaped curve when graphed on the function by scale!